mixtree

Introduction

The mixtree package provides a statistical framework for comparing sets of trees (“forests”). The function tree_test(), can apply various hypothesis testing approaches to assess differences between forests. While currently supporting transmission trees, future updates will expand functionality to include phylogenetic trees and, graphs more generally.

Methods

The $\chi^2$ test compares the absolute frequencies of edges between forests. PERMANOVA compares the overall topological structure of trees between forests based on pairwise distances.

Both methods test the null hypothesis that the forests are drawn from the same generative process.

Input Requirements

Each input set must be a list of data frames. Every data frame represents a tree and must contain exactly two columns:

from: The parent node.
to: The child node.

make_tree is a helper function that simulates a DAG with the number of branches per node drawn from a Poisson distribution with $\lambda$ = R when stochastic = TRUE

library(mixtree)
make_tree(20, R = 2, stochastic = TRUE, plot = TRUE)

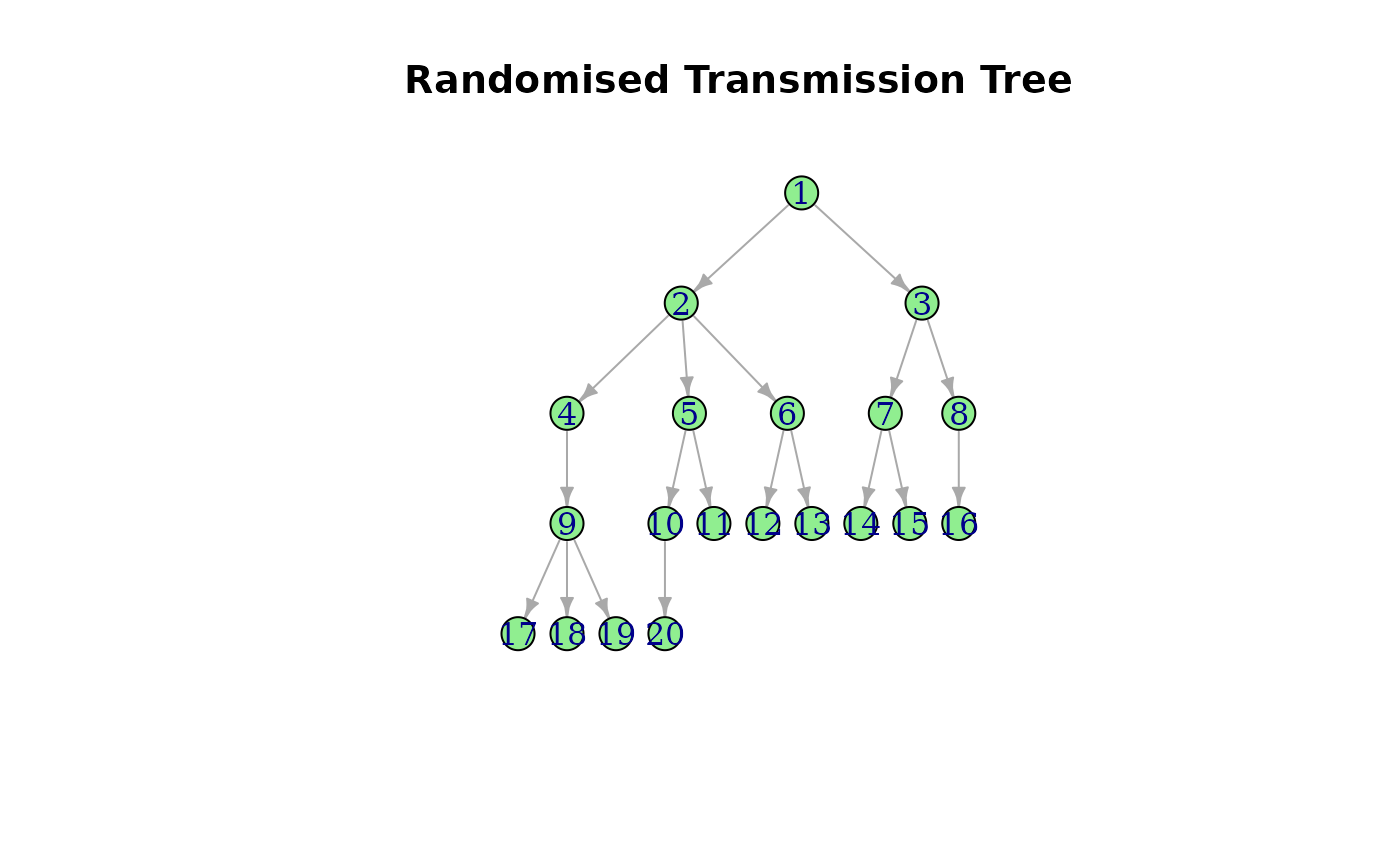
#> IGRAPH c1ee958 D--- 20 19 -- 
#> + edges from c1ee958:
#>  [1]  1-> 2  1-> 3  2-> 4  2-> 5  2-> 6  3-> 7  3-> 8  4-> 9  5->10  5->11
#> [11]  6->12  6->13  7->14  7->15  8->16  9->17  9->18  9->19 10->20

Usage

The unified interface is provided by the tree_test() function. Users can supply two or more sets of trees and select the desired testing method via the method parameter.

PERMANOVA

set.seed(123)
# Generate 100 trees with R₀ = 2
chainA <- lapply(1:100, function(i){
  make_tree(20, R = 2, stochastic = TRUE) |>
    igraph::as_long_data_frame()
})

# Generate 100 trees with R₀ = 4
chainB <- lapply(1:100, function(i){
  make_tree(20, R = 4, stochastic = TRUE) |>
     igraph::as_long_data_frame()
})

tree_test(chainA, chainB, method = "permanova")
#> Permutation test for adonis under reduced model
#> Permutation: free
#> Number of permutations: 999
#> 
#> (function (formula, data, permutations = 999, method = "bray", sqrt.dist = FALSE, add = FALSE, by = NULL, parallel = getOption("mc.cores"), na.action = na.fail, strata = NULL, ...) 
#>           Df SumOfSqs      R2      F Pr(>F)    
#> Model      1     8052 0.14429 33.388  0.001 ***
#> Residual 198    47750 0.85571                  
#> Total    199    55802 1.00000                  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The p-value is below the 5% significance level, we reject the null hypothesis of no difference.

Chi-Square Test

tree_test(chainA, chainB, method = "chisq", test_args = list(simulate.p.value = TRUE, B = 999))
#> 
#>  Pearson's Chi-squared test with simulated p-value (based on 999
#>  replicates)
#> 
#> data:  count data
#> X-squared = 1791.2, df = NA, p-value = 0.001

Advanced Usage

The tree_test() function accepts additional parameters to customise the testing process:

within_dist: A function to compute pairwise distances within a tree (used with PERMANOVA). Default is patristic().
between_dist: A function to compute the distance between two trees (used with PERMANOVA). Default is euclidean().
test_args: A list of extra arguments passed to the underlying test function (i.e. vegan::adonis2,stats::chisq.test, or stats::fisher.test).

Using Custom Distance Functions

The package supports custom distance functions, such as the MRCI depth measure described in Kendall et al.(2018). See also the vignette from treespace.

library(treespace)
mrciDepth <- function(tree) {
 treespace::findMRCIs(as.matrix(tree))$mrciDepths
}
tree_test(chainA, chainB, within_dist = mrciDepth)

Note

Randomly shuffling node IDs will not affect the PERMANOVA test results if the distance functions are invariant to node labelling (e.g. patristic()). However, if a custom function depends on the order or specific labels of nodes, then shuffling could influence the results (e.g. treespace::findMRCIs).

chainA <- lapply(1:50, function(i) {
  make_tree(20, R = 2, stochastic = TRUE)
})
chainB <- lapply(1:50, function(i) {
  df <- mixtree:::shuffle_graph_ids(chainA[[i]]) |>
    igraph::as_long_data_frame()
  subset(df, select = c("from", "to"))
})
chainA <- lapply(chainA, igraph::as_long_data_frame)
  
tree_test(chainA, chainB, method = "permanova")
#> Permutation test for adonis under reduced model
#> Permutation: free
#> Number of permutations: 999
#> 
#> (function (formula, data, permutations = 999, method = "bray", sqrt.dist = FALSE, add = FALSE, by = NULL, parallel = getOption("mc.cores"), na.action = na.fail, strata = NULL, ...) 
#>          Df SumOfSqs R2  F Pr(>F)
#> Model     1        0  0  0      1
#> Residual 98    32796  1          
#> Total    99    32796  1

# In contrast, the Chi-Square test will reject the null as it compare edge frequencies
tree_test(chainA, chainB, method = "chisq")
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  count data
#> X-squared = 849.55, df = 193, p-value < 2.2e-16

Future Developments

While the current implementation focuses on transmission trees, the package is designed with extensibility in mind. Future versions will support phylogenetic trees and graphs more generally.

Cyril Geismar

2025-12-02